2
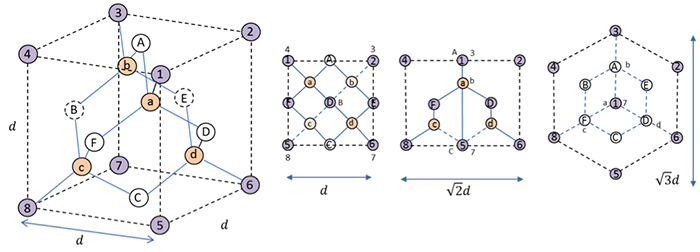
ダイヤモンドの充填率の求め方を教えてください! 一辺は356×10^8cmです! ダイヤモンド構造の原子球の充填率を求めよ。図をかけ。そして、Siの原子密度を求めよ。さらに、Siが正四面体配位を持つ共有結合を取る理由を説明せよ。ダイヤモンド型構造 ダイヤモンドでは,結合を4つ持ったテトラポッド型の炭素原子どうしが 共有結合で結合し,立体的な網目構造を作っている.炭素原子はsp3混 成状態を取っている.その他に,Si,Geもダイヤモンド型構造を取る.
ダイヤモンド構造 充填率 求め方
ダイヤモンド構造 充填率 求め方-ダイヤモンドには単位セルあたり8個の原子があるので、ダイヤモンドの充填率の方程式は次のようになります。 充填率= 8 x(V原子)/ V単位セル 原子の体積を方程式に代入します。 原子が球状であると仮定すると、体積は次のとおりです。 V = 4/3×π×r 3 この記事では、ミラー指数を用いて面や方向をどのように表すかを学ぶ。 なお、ほとんどの金属は面心立方構造・体心立構造・六方最密充填構造のいずれかの構造を取るため、以下では立方晶および六方晶について考えることにする。 目次 1 立方晶の

ダイヤモンド型結晶の問題解法 覚えるべき事4選 化学受験テクニック塾
単位格子の充填率を計算する 結晶は原子が完全に詰まっているわけではなく隙間があります。 結晶にどのくらい原子が詰まっているかを表す指標として結晶体積における原子体積の割合である充填率が用いられます。 ここでは単純立方格子、体心立方0' C# 0'4C/A, 0'4C &5 3 D @ =>1< ダイヤモンド構造は基本となる面心立方 ダイアモンド構造結晶について ダイアモンド構造のシリコン結晶をとある面から二次元的に投影したとき、 投影面中を充填する格子の割合が最大となる面(ミラー指数)は何でしょうか? また、その時の二次元的な充填率はいくらでしょうか?
充填率 とは、単位格子の体積に占める原子の体積の割合である。 上の「体心立方格子に含まれる原子の数」でやったように、体心立方格子は単位格子中に2コの原子を含んでいるので、次のような式を立てることができる。 単位格子の1辺の長さ(格子定数充填率を求めるためには,単位格子の長さa を原子の半径r で表す必要がある.そのためには,単位格子中の 2個の直角三角形を用いる. 一つ目の三角形は単位格子2辺と面対角線がつくる三角形で,単位格子と面対角線の長さに関係する.面対角これより、体心立方格子の充填率は約 68% 、面心立方格子の充填率は約 74% であることが分かります。面心立方格子は最も密な構造なので、この 74% が充填率の極大であることも分かります。 なお、六方最密構造の充填率は、次のようにして求めます。
ダイヤモンド構造 充填率 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  |  |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「ダイヤモンド構造 充填率 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 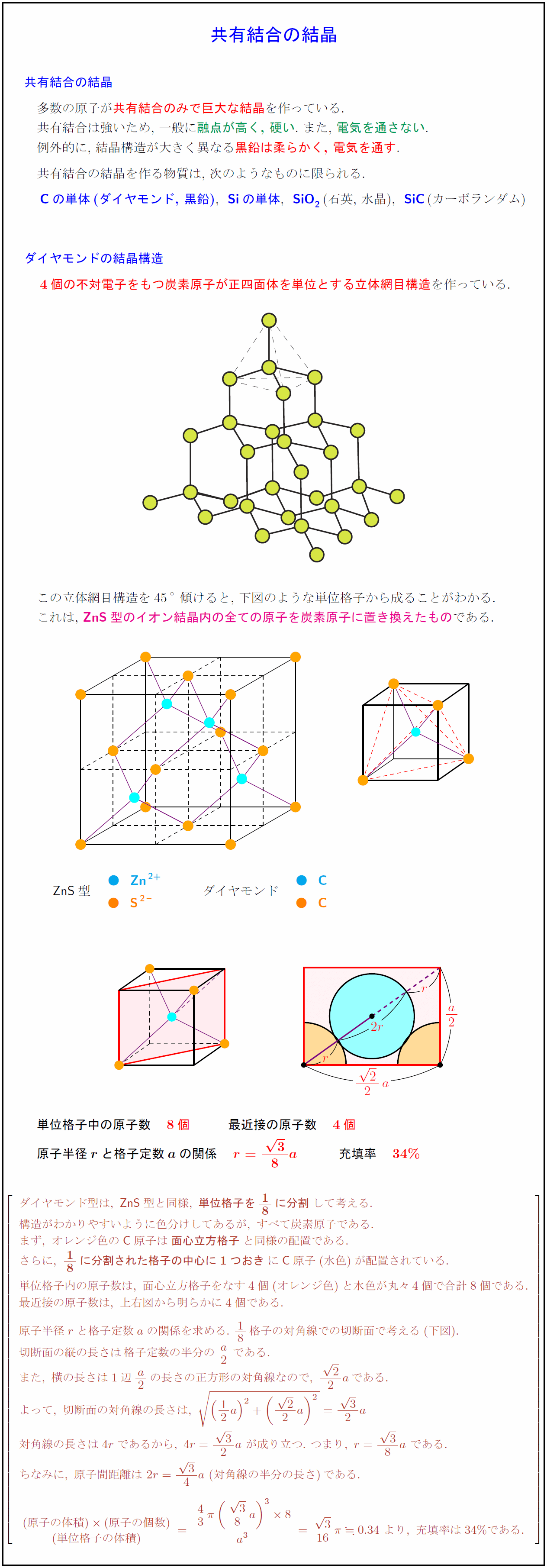 |
ダイヤモンドには単位セルあたり8個の原子があるので、ダイヤモンドの充填率の方程式は次のようになります。 充填率= 8 x(V原子)/ V単位セル 原子の体積を方程式に代入します。 原子が球状であると仮定すると、体積は次のとおりです。 V = 4/3×π×r 3 充填率 結晶では、結晶格子の格子点に剛体球をおいたときに格子の体積のうち球で占められる割合を 充填率 という。 つまり充填率は、結晶の体積のうち、原子がどのくらいの割合を占めているかを表す値である。 充填率を求める場合は、原子を剛体球
Incoming Term: ダイヤモンド構造 充填率 求め方,




0 件のコメント:
コメントを投稿